La función de densidad de probabilidad (FDP) es un concepto fundamental en la estadística y la teoría de probabilidades, crucial para entender cómo se distribuyen los datos en diversas situaciones. Si te has preguntado cómo aplicar estos principios en situaciones prácticas o académicas, estás en el lugar correcto. En este artículo, te ofreceremos una guía completa sobre los ejercicios resueltos de función de densidad de probabilidad, cubriendo desde los conceptos básicos hasta ejemplos más complejos que te ayudarán a consolidar tus conocimientos. Aprenderás a identificar funciones de densidad, calcular probabilidades, y aplicar estos conceptos en diferentes contextos. Así que, si estás listo para profundizar en este fascinante tema, ¡vamos a empezar!
¿Qué es una Función de Densidad de Probabilidad?
Una función de densidad de probabilidad es una función que describe la probabilidad relativa de que una variable aleatoria continua tome un valor específico. A diferencia de las variables discretas, donde se puede calcular la probabilidad de un evento específico, en las variables continuas se trabaja con intervalos. La FDP se utiliza para determinar la probabilidad de que una variable aleatoria caiga dentro de un rango determinado de valores.
Características de la Función de Densidad de Probabilidad
Para comprender mejor la FDP, es esencial conocer sus características clave:
- Siempre no negativa: La FDP nunca toma valores negativos. Esto se debe a que la probabilidad no puede ser menor que cero.
- Área total igual a uno: La integral de la FDP sobre todo el espacio de la variable aleatoria es igual a uno. Esto asegura que se considera toda la probabilidad posible.
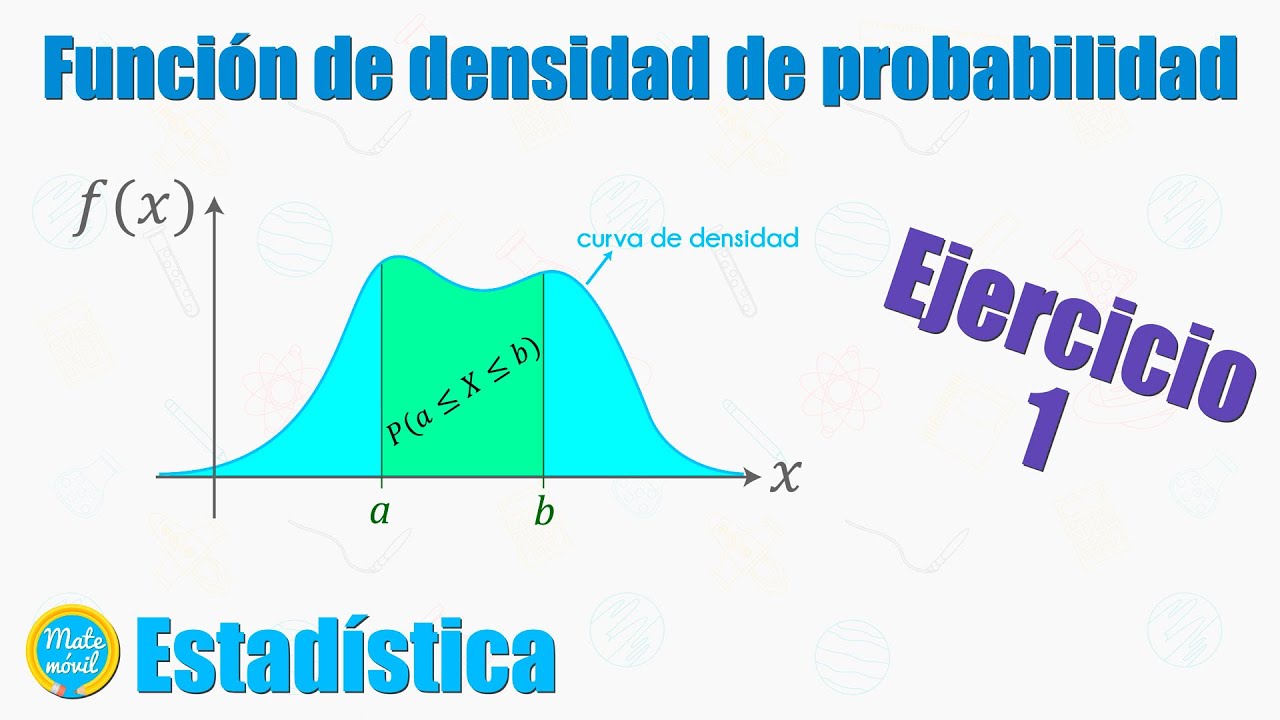
- Probabilidad en intervalos: La probabilidad de que la variable aleatoria tome un valor en un intervalo se calcula como el área bajo la curva de la FDP en ese intervalo.
Ejemplo de una Función de Densidad de Probabilidad
Consideremos la función de densidad de probabilidad de una variable aleatoria continua X, que sigue una distribución normal con media μ y desviación estándar σ. La fórmula es:
f(x) = (1 / (σ√(2π))) * e^(-((x – μ)²) / (2σ²))
En este caso, la FDP es una campana simétrica, donde la media, la mediana y la moda coinciden. Esto permite calcular probabilidades para intervalos, por ejemplo, la probabilidad de que X esté entre a y b se obtiene integrando f(x) de a a b.
Cálculo de Probabilidades con Funciones de Densidad
Una vez que comprendes la FDP, el siguiente paso es aprender a calcular probabilidades. Este proceso implica determinar el área bajo la curva de la FDP en un intervalo específico. Aquí, te mostraremos cómo hacerlo con un ejemplo práctico.
Ejemplo Práctico: Cálculo de Probabilidades
Supongamos que tenemos una variable aleatoria X que sigue una distribución normal con μ = 100 y σ = 15. Queremos calcular la probabilidad de que X esté entre 90 y 110. Para ello, seguimos estos pasos:
- Calculamos los valores Z para los límites del intervalo usando la fórmula: Z = (X – μ) / σ.
- Para X = 90: Z1 = (90 – 100) / 15 = -0.67.
- Para X = 110: Z2 = (110 – 100) / 15 = 0.67.
- Consultamos la tabla de la distribución normal para encontrar las probabilidades correspondientes a Z1 y Z2.
- Restamos la probabilidad de Z1 de la probabilidad de Z2 para encontrar la probabilidad total en el intervalo.
Este método se puede aplicar a cualquier función de densidad de probabilidad, no solo a la normal, siempre y cuando se tenga la función adecuada y se sigan los pasos de integración.
Tipos Comunes de Funciones de Densidad de Probabilidad
Existen diversas funciones de densidad de probabilidad que se utilizan en diferentes contextos. A continuación, exploraremos algunas de las más comunes.
Distribución Normal
La distribución normal, también conocida como la distribución de Gauss, es quizás la más conocida. Se caracteriza por su forma de campana y es utilizada en muchas disciplinas, desde la psicología hasta la economía. En esta distribución, la mayoría de los valores se agrupan alrededor de la media, y la probabilidad de valores extremos disminuye rápidamente.
Distribución Exponencial
La distribución exponencial es otra función de densidad importante, utilizada comúnmente para modelar el tiempo entre eventos en un proceso de Poisson. Por ejemplo, puede usarse para modelar el tiempo entre llegadas de clientes a una tienda. Su función de densidad es:
f(x) = λe^(-λx), donde λ es la tasa de ocurrencia.
Distribución Uniforme
La distribución uniforme se caracteriza por tener la misma probabilidad en un intervalo específico. Por ejemplo, si lanzas un dado, cada número tiene la misma probabilidad de aparecer. Su función de densidad es:
f(x) = 1 / (b – a), donde [a, b] es el intervalo en el que la variable aleatoria toma valores.
Ejercicios Resueltos de Función de Densidad de Probabilidad
Ahora que hemos cubierto los conceptos básicos, es hora de poner en práctica lo aprendido. A continuación, te presentamos varios ejercicios resueltos que te ayudarán a afianzar tus conocimientos sobre funciones de densidad de probabilidad.
Ejercicio 1: Cálculo de Probabilidad en una Distribución Normal
Imagina que la altura de los estudiantes de una universidad sigue una distribución normal con media 170 cm y desviación estándar 10 cm. Queremos calcular la probabilidad de que un estudiante seleccionado al azar mida entre 160 cm y 180 cm.
- Calculamos los valores Z: Z1 para 160 cm y Z2 para 180 cm.
- Usamos la fórmula: Z = (X – μ) / σ.
- Encontramos los valores de Z y consultamos la tabla para obtener las probabilidades.
- Restamos las probabilidades para encontrar la probabilidad total.
Ejercicio 2: Aplicación de la Distribución Exponencial
Consideremos un caso donde la tasa de llegada de clientes a un servicio es de 2 por hora. La variable aleatoria que representa el tiempo entre llegadas sigue una distribución exponencial. Queremos calcular la probabilidad de que el tiempo entre llegadas sea menor a 30 minutos.
- Identificamos λ como 2 llegadas por hora (o 1 cada 30 minutos).
- Usamos la función de densidad para calcular la probabilidad.
Consejos para Resolver Ejercicios de Función de Densidad de Probabilidad
Resolver ejercicios de función de densidad de probabilidad puede parecer complicado al principio, pero con algunos consejos prácticos, puedes hacerlo más fácilmente. Aquí te dejamos algunos tips:
- Comprende la Teoría: Antes de intentar resolver ejercicios, asegúrate de entender los conceptos básicos de la función de densidad y cómo se aplican.
- Practica Regularmente: La práctica es clave. Cuanto más practiques, más cómodo te sentirás con los diferentes tipos de funciones y sus aplicaciones.
- Utiliza Herramientas: Existen muchas calculadoras y software que pueden ayudarte a realizar cálculos complejos de manera más sencilla.
- Estudia Ejercicios Resueltos: Analiza ejercicios resueltos para comprender cómo se aplican los conceptos en situaciones prácticas.
¿Qué es una función de densidad de probabilidad?
Una función de densidad de probabilidad es una función matemática que describe la probabilidad de que una variable aleatoria continua tome un valor dentro de un intervalo determinado. A diferencia de las variables discretas, en las continuas se trabaja con áreas bajo la curva de la función.
¿Cómo se calcula la probabilidad en una función de densidad?
La probabilidad se calcula integrando la función de densidad sobre el intervalo de interés. El resultado de esta integral representa el área bajo la curva de la FDP, lo que equivale a la probabilidad de que la variable aleatoria caiga dentro de ese rango.
¿Qué tipos de distribuciones existen en funciones de densidad?
Existen varias distribuciones importantes en funciones de densidad, entre las que se incluyen la distribución normal, exponencial y uniforme. Cada una tiene características y aplicaciones específicas, dependiendo del tipo de datos que se analicen.
¿Cuál es la importancia de la función de densidad de probabilidad?
La función de densidad de probabilidad es fundamental en estadística porque permite modelar y entender la variabilidad de los datos. Ayuda a calcular probabilidades, realizar inferencias estadísticas y tomar decisiones basadas en datos.
¿Cómo se relaciona la FDP con la estadística descriptiva?
La FDP complementa la estadística descriptiva al proporcionar una representación más detallada de cómo se distribuyen los datos. Mientras que la estadística descriptiva se centra en resumir y describir datos, la FDP permite entender la probabilidad de diferentes resultados.
¿Puedo aplicar la función de densidad a datos discretos?
No, la función de densidad de probabilidad se aplica únicamente a variables aleatorias continuas. Para variables discretas, se utilizan funciones de masa de probabilidad, que asignan probabilidades a valores específicos.
¿Cómo puedo mejorar en la resolución de problemas de funciones de densidad?
Mejorar en la resolución de problemas de funciones de densidad requiere práctica constante. Estudia ejemplos, resuelve ejercicios y, si es posible, utiliza software que te ayude a realizar cálculos. También puedes unirte a grupos de estudio o foros en línea donde se discutan estos temas.