En el vasto mundo de la geometría y la matemática, el concepto de segmento es fundamental, pero a menudo se pasa por alto en las discusiones cotidianas. ¿Qué es exactamente un segmento? ¿Por qué es importante entender sus características clave? Un segmento no solo es una parte de una línea; es un elemento que tiene aplicaciones en diversas disciplinas, desde la arquitectura hasta la física y la informática. En este artículo, exploraremos el concepto de segmento, sus propiedades esenciales y cómo pueden influir en nuestro entendimiento del espacio y la forma. Si quieres profundizar en este tema y conocer las características que no debes pasar por alto, sigue leyendo. Aquí encontrarás información valiosa que te ayudará a apreciar la importancia de los segmentos en nuestra vida diaria y en el mundo académico.
Definición de Segmento
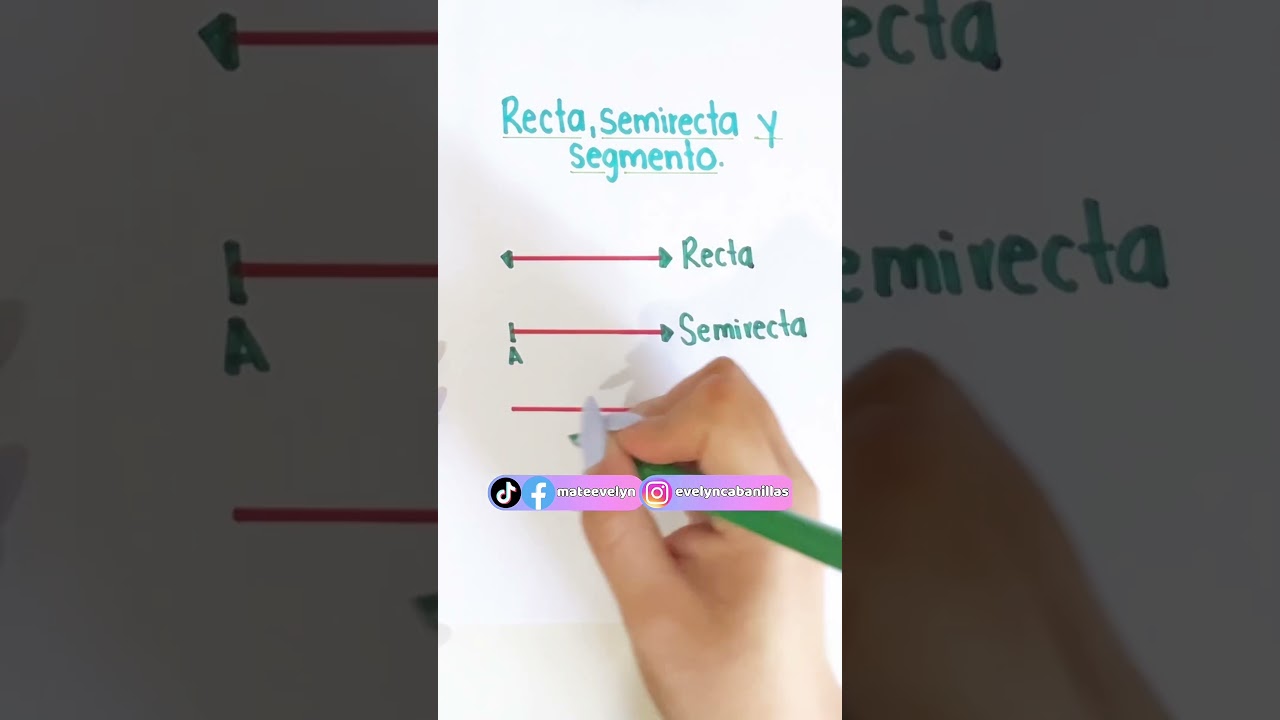
El segmento es una parte de una línea recta que está delimitada por dos puntos finales. A diferencia de una línea que se extiende infinitamente en ambas direcciones, un segmento tiene una longitud finita y específica. Estos dos puntos, conocidos como extremos, son fundamentales para definir el segmento y se denotan comúnmente como A y B, lo que se representa como el segmento AB. En términos simples, un segmento se puede visualizar como una cuerda estirada entre dos puntos, y es esta finitud lo que le da una serie de características únicas.
1 Propiedades de un Segmento
Los segmentos tienen varias propiedades interesantes que los distinguen de otros elementos geométricos. Por ejemplo:
- Longitud: Cada segmento tiene una longitud específica que se puede medir en unidades como metros o centímetros.
- Colinealidad: Dos segmentos son colineales si están en la misma línea recta, lo que significa que pueden extenderse en la misma dirección.
- División: Un segmento puede ser dividido en partes más pequeñas, lo que es fundamental en la construcción y el diseño.
Entender estas propiedades es esencial para cualquier aplicación práctica del concepto de segmento, ya sea en matemáticas puras o en aplicaciones del mundo real.
2 Ejemplos de Segmentos en la Vida Cotidiana
Los segmentos están presentes en nuestra vida diaria de formas que a menudo no reconocemos. Por ejemplo, considera una regla: cada sección entre dos marcas en la regla es un segmento. Otro ejemplo puede ser el camino que recorres de tu casa a la tienda; cada tramo de ese camino puede ser considerado un segmento. Estos ejemplos ayudan a ilustrar cómo los segmentos son más que simples conceptos matemáticos; son partes integrales de nuestro entorno.
Clasificación de Segmentos
Los segmentos pueden clasificarse de diversas maneras, y esta clasificación puede variar dependiendo del contexto. A continuación, exploraremos dos clasificaciones importantes: la longitud y la orientación.
1 Segmentos según su Longitud
Los segmentos pueden ser clasificados en tres categorías principales según su longitud:
- Segmentos Cortos: Estos son segmentos que miden menos de un metro y son comunes en aplicaciones cotidianas, como la medición de objetos pequeños.
- Segmentos Medianos: Con longitudes que oscilan entre uno y diez metros, estos segmentos se utilizan a menudo en trabajos de construcción y diseño de interiores.
- Segmentos Largos: Aquellos que superan los diez metros, como los utilizados en la construcción de edificios o puentes, son cruciales en la ingeniería y la arquitectura.
Conocer la clasificación de los segmentos según su longitud puede ser útil para profesionales que necesitan medir y calcular distancias en sus proyectos.
2 Segmentos según su Orientación
La orientación de un segmento se refiere a su dirección en el espacio. Los segmentos pueden ser:
- Horizontales: Orientados de izquierda a derecha o viceversa.
- Verticales: Orientados de arriba hacia abajo.
- Diagonales: Que se extienden en ángulos que no son ni horizontales ni verticales.
La orientación es un aspecto crucial en la geometría, ya que afecta cómo se relacionan los segmentos entre sí y con otros elementos en un plano.
Aplicaciones de los Segmentos en la Matemática
El concepto de segmento es esencial en varias ramas de la matemática. Su aplicación no se limita a la geometría; también juega un papel importante en el álgebra y la trigonometría.
1 Segmentos en Geometría
En geometría, los segmentos son fundamentales para la construcción de figuras. Por ejemplo, un triángulo está formado por tres segmentos que se conectan en sus extremos. Además, los segmentos son cruciales para calcular áreas y perímetros. La longitud de los segmentos también se utiliza en teoremas como el teorema de Pitágoras, que relaciona los lados de un triángulo rectángulo.
2 Segmentos en Álgebra y Trigonometría
En álgebra, los segmentos se utilizan para representar relaciones entre variables. Por ejemplo, en una gráfica, los segmentos pueden representar la relación entre dos variables. En trigonometría, los segmentos son esenciales para calcular ángulos y distancias, utilizando funciones como el seno, coseno y tangente. Esta interconexión entre segmentos y otras áreas matemáticas demuestra su versatilidad y su importancia en el estudio de las matemáticas.
Segmentos en la Ingeniería y la Arquitectura
En la ingeniería y la arquitectura, los segmentos son más que simples conceptos; son la base de la planificación y construcción de estructuras. La precisión en la medición de segmentos es crucial para garantizar la estabilidad y la funcionalidad de un edificio o una infraestructura.
1 Diseño Estructural
Los ingenieros utilizan segmentos para diseñar estructuras que soporten cargas. Por ejemplo, en un puente, cada segmento de la estructura debe ser calculado para asegurar que pueda soportar el peso del tráfico. Los ingenieros civiles realizan cálculos precisos sobre la longitud y la resistencia de cada segmento, garantizando la seguridad y la durabilidad de la construcción.
2 Planificación Urbana
La planificación urbana también depende del concepto de segmento. Los urbanistas utilizan segmentos para diseñar calles, parques y espacios públicos. La organización de estos segmentos influye en la circulación del tráfico y la accesibilidad de los servicios. Un buen diseño de segmentos puede mejorar la calidad de vida de los habitantes de una ciudad.
Segmentos en el Diseño Gráfico
En el ámbito del diseño gráfico, los segmentos juegan un papel crucial en la creación de imágenes y composiciones. Los diseñadores utilizan segmentos para formar líneas, formas y patrones, que son elementos esenciales en la comunicación visual.
1 Creación de Líneas y Formas
Los segmentos son utilizados para crear líneas que definen formas. Por ejemplo, un cuadrado está compuesto por cuatro segmentos que forman sus lados. En el diseño gráfico, la manipulación de estos segmentos permite a los diseñadores experimentar con diferentes estilos y composiciones. La longitud y la orientación de los segmentos pueden alterar la percepción visual de una imagen.
2 Patrones y Texturas
Además, los segmentos son fundamentales en la creación de patrones y texturas. Al repetir segmentos en diferentes orientaciones y longitudes, los diseñadores pueden crear efectos visuales atractivos. Esta técnica es común en el diseño de telas, papel tapiz y gráficos digitales, donde los segmentos se utilizan para añadir profundidad y complejidad a las composiciones.
Errores Comunes al Trabajar con Segmentos
Al estudiar y trabajar con segmentos, es fácil cometer errores que pueden llevar a malentendidos o cálculos incorrectos. Aquí discutiremos algunos de los errores más comunes y cómo evitarlos.
1 Confundir Segmentos con Líneas
Uno de los errores más comunes es confundir un segmento con una línea. Mientras que un segmento tiene dos extremos y una longitud definida, una línea se extiende indefinidamente. Es crucial recordar esta diferencia al realizar cálculos o construir figuras geométricas.
2 Medición Incorrecta
Otro error frecuente es la medición incorrecta de la longitud de un segmento. Al usar herramientas de medición, como reglas o cintas métricas, es importante asegurarse de que se está midiendo desde el extremo correcto. Una medición errónea puede afectar todo el proyecto, desde el diseño hasta la construcción.
La Importancia de Comprender el Concepto de Segmento
Comprender el concepto de segmento es esencial en una variedad de campos, desde la matemática hasta la ingeniería y el diseño. La capacidad de medir, clasificar y aplicar segmentos de manera efectiva puede tener un impacto significativo en la calidad y la precisión de los proyectos. Al dominar este concepto, no solo mejorarás tus habilidades matemáticas, sino que también podrás aplicar este conocimiento en situaciones del mundo real.
¿Qué es un segmento en geometría?
Un segmento en geometría es una parte de una línea recta que está delimitada por dos puntos finales. Tiene una longitud específica y se denota generalmente como AB, donde A y B son los extremos del segmento. Los segmentos son fundamentales para construir figuras geométricas y realizar cálculos de distancia.
¿Cuáles son las principales propiedades de un segmento?
Las principales propiedades de un segmento incluyen su longitud, colinealidad y la capacidad de ser dividido en partes más pequeñas. Cada segmento tiene una longitud específica que puede ser medida, y puede ser colineal con otros segmentos si están en la misma línea recta.
¿Cómo se utilizan los segmentos en la arquitectura?
En la arquitectura, los segmentos son esenciales para el diseño y la construcción de estructuras. Los arquitectos utilizan segmentos para calcular longitudes y determinar cómo se conectan diferentes partes de un edificio, asegurando que sean estables y funcionales.
¿Qué errores debo evitar al trabajar con segmentos?
Al trabajar con segmentos, es importante no confundirlos con líneas, ya que los segmentos tienen extremos y longitud definida. También es crucial medir correctamente la longitud del segmento, ya que una medición incorrecta puede afectar el resultado final de un proyecto.
¿Cómo se relacionan los segmentos con otras áreas de las matemáticas?
Los segmentos están interrelacionados con otras áreas de las matemáticas, como la geometría, el álgebra y la trigonometría. Por ejemplo, en geometría, los segmentos son utilizados para construir figuras, mientras que en trigonometría, se utilizan para calcular distancias y ángulos.
¿Por qué es importante entender el concepto de segmento?
Entender el concepto de segmento es crucial porque se aplica en muchas disciplinas, desde la matemática hasta la ingeniería y el diseño gráfico. Un dominio sólido de este concepto puede mejorar la precisión y la calidad de los proyectos en los que trabajes.
¿Existen aplicaciones de segmentos en la vida diaria?
Sí, los segmentos están presentes en nuestra vida diaria en diversas formas. Por ejemplo, cada tramo de una carretera puede ser considerado un segmento, así como las líneas que forman los objetos en el diseño gráfico. Reconocer estos segmentos puede ayudarnos a entender mejor nuestro entorno y las estructuras que nos rodean.